Sign up for daily news updates from CleanTechnica on email. Or follow us on Google News!
The following is a theoretical comparative analysis for vehicle(s) driving between stations. The values for number of packs per vehicle are comparative and not absolute.
In the real world, cars are not charged solely at fast charging stations, and the number of fast charging stations per vehicles is much less than one. The same is true for swap stations. Cars are primarily charged at low power at home or near place of residence. The percentage of trips more than 100 miles is very low.
Cars more often travel short daily distances. Trucks have different use profiles and higher daily use rates. Taxis also have high daily use rates.
Electric vehicle charging station planning can be seen from the perspective of vehicles along a single route, multiple routes, and in network patterns of various types — mesh, grid, star, and more. The simplest sub-pattern is a route that is a continuous line connected in an unbroken sequence. All the large map routes — like mesh or star — are supersets of a line. Taken as it is, a line route can be analyzed along multiple dimensions, considering the number of vehicles, time, distance, and the nature of the charging along the route. In a trivial case, a vehicle originates at a location with a pack and travels the route to destination and returns successfully, given the round trip route is shorter than the vehicle range and the vehicle is fully charged at the start. There must be a charger at either the destination or origin to start or repeat this route. The nature of routing is iterative and cyclical. In complex routing networks, routes may superpose. In a repeating, scheduled routing system, charging requirements are deterministic. In a randomly varying system, routing acquires a probabilistic nature.
The line route provides relationships between variables. In particular, distances between stations, numbers of chargers required, and route times. The relationship between origin times, arrival times, number of chargers required, and arrival coincidence can be predicted.
If formulas are not for you, you can jump down to section on “Swap Station Continuous Operation” for some general conclusions.
The simple case can be expanded to include multiple vehicles at the origin point. For fast and slow charging, the number of packs, P, is just the number of vehicles, T.
P = T
If route start time is simultaneous, the number of chargers per station, C, required on a route must increase by the number of trucks, T, if all trucks do not wait for charging.
C = T, for no charger wait.
If the route is lengthened, charging stations must be placed at intervals Sd less than vehicle range, R.
Sd < R ; Sd charging station distance, R vehicle range.
The number of stations must increase with distance, where the number of stations is S, and route distance is D, the range R.
S = D/R – 1, where S is next higher whole number.
Charging time, Ct, must be less than travel time between stations. S is a discrete variable, with integer values.
The number of chargers scales with the number of trucks and the number of stations.
C = T, for simultaneous truck arrivals, one station.
Total chargers, C, for the route, must be number of chargers per station × stations. Chargers per station equals Tsim, the number of vehicles arriving at a station simultaneously.
Tsim = Cs, where Tsim is the number of simultaneous vehicle arrivals. Cs is chargers per station.
C = Tsim × S
If route start time is not simultaneous, but spread out over time, and if there are no returning trucks on the route, there will be no simultaneous charging. If start times, Tstart are spaced at longer intervals than station charging time, Ct, each vehicle will charge and leave before the next vehicle in line arrives. In this manner, vehicles may be spaced in time along the route so there is always a vehicle leaving and arriving at a charging station.
Tstart > Ct, for no charger arrival conflict, where Ct is charging time, Tstart is starting interval
If vehicles return from destination immediately, returning vehicles may arrive at charging stations simultaneous with vehicles en route to destination, resulting in two vehicles charging at the same time, increasing the chargers per station by 2×. Additional fast chargers are necessary at destination if vehicle return is fast. Chargers at destination would then be Tsim.
Any time delay in return will avoid outbound and return vehicle simultaneity, but charger crowding and wait times cannot be avoided unless there is sufficient time for both vehicles to charge. To do that, the chain of outbound and returning vehicles must have one vehicle en route to a charger on the return link, and one on the outbound link, but their arrival at stations must be spaced apart such that each vehicle arrives at intervals > Ct, charging time.
Round Trip Chain & Charge Rate
For vehicles traveling in both directions, in order to avoid simultaneous charging and no overlap in charging times, a return delay of one charging time may be added at destination.
From this, we can determine that more vehicles may be added outbound without overlapping inbound by adding an interval in the chain of vehicles. Continuing, we realize that for full optimization of the loop, and because there are trucks outbound and inbound, we may add vehicles up to a limit by travel time between stations, Sd/v, where Sd is station distance, and v is vehicle velocity, if all vehicles travel at the speed limit.
The vehicles are in a continuous departure and arrival chain, or chain departure.
St is driving time between stations.
St = Sd/v where Sd is station distance, Sd < R, and St is driving time between stations, and v is velocity, the speed limit, and all vehicles travel the same speed.
The maximum number of trucks, Tchain, that the route can handle is:
Tchain = St/Ct = Sd/(v x Ct); Ct is charging time, v is velocity the speed limit, Sd station distance, and Tchain is a whole number dropping remainder. Since the limit of station distance is R,
Tchain < R/(v x Ct)
The maximum chargers per station Cs, is Tsim, the number of arriving trucks, and the minimum number of chargers per station is 1.
1 <= C <= Tsim is the range of values of C, total chargers.
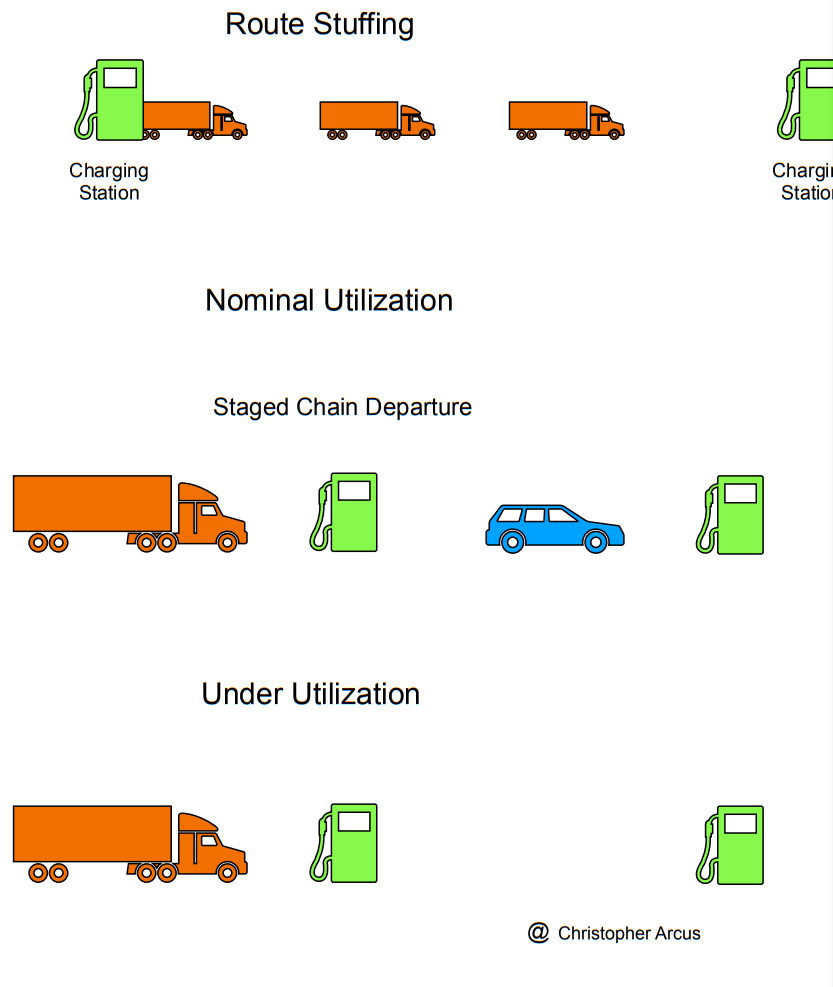
Results extend to fast charging and slow charging. If the maximum trucks Tchain was attained, every fast charger would be operating simultaneously at the maximum power from the power source.
If fast charging stations are at full utilization, with one vehicle per charger, the number of vehicles is proportional to stations, S and chargers per station, Cs.
T = Cs x S, full utilization
If vehicles start in a single pulse equal to the number of chargers per station, and all but one stations are empty,
T = Cs, where Cs is the number of chargers per station.
If there are S stations, (S – 1) x C chargers are unused.
The total number of chargers on a route is S x Cs.
C = S x Cs
Result:
For full utilization, there is one charger per vehicle. C = T.
If there is underutilization, there is more than one charger per vehicle. The number of chargers and stations grows with route length and chargers per station.
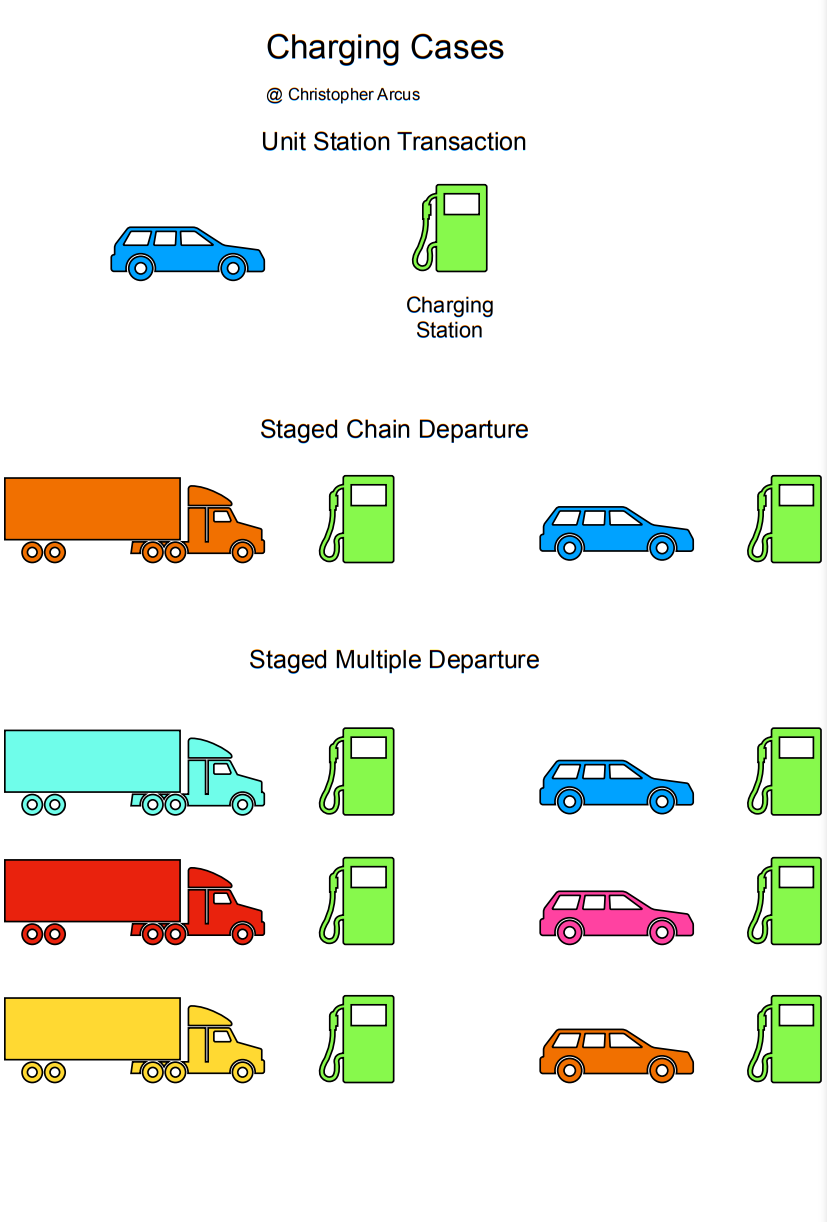
Battery Swap
For battery swap, the equation for number of stations is the same, given by route distance and range. With swap, the number of packs, P, needs consideration. There must be a charged pack at truck arrival in each case, and a pack is dropped off at each station.
Maximum spacing distance between stations is the same,
Sd < R ; Sd Charging station distance, R vehicle range.
Swap offers the possibility of carrying fewer packs on board if station spacing distance is lower than this limit.
This inequality still holds true.
S > D/R , where S is the next higher whole number, D distance between stations.
Charging time, Ct, must be less than travel time.
For battery swap, the inequality still holds, only if charging time equals driving time between stations, St, Ct = St.
Cs = T (simultaneous), for no charger wait. Cs is chargers per station.
Fewer chargers may be needed within the swap station if faster charging is done, but since Swap may be slow charged, we can continue without further analysis in this matter.
For our purposes, the number of chargers is not as important. What is important is the number of packs. If simultaneous arrival happens, the number of packs, P, must increase to avoid waits. In the swap slow charge case, with charging times maximized, vehicles serviced at each station without wait is the number of packs at each station. If swap packs are slow charged, and swap packs are depleted, either the wait becomes the slow charging interval or means such as a fast charger may be accessed, reverting to fast charge mathematics. Because the interval between charging is related to range and driving time, overloading points the way to using a cascade of Swap, Fast Charge, and Slow Charge. When all charging resources are saturated, wait happens.
For continuous staggered departure, arrival of single vehicles at each station,
P = S + T,
where P is packs, and T is the number of vehicles, S is stations, because one pack is on the truck and the other is in the swap station at every transaction. If all stations are doing transactions, this is the case.
For routes longer than range R, the number of stations increases.
S = D/R – 1, where D is route distance and S is the next highest whole number, and one vehicle on a route.
For one vehicle or one set of vehicles arriving simultaneously at one station on a route,
P = 2T,
For 1 < D/R < 2, or S = 1, in other words only one station en route, one vehicle, because there is only one station, one pack per vehicle, and one pack arriving with each vehicle.
For continuous multiple vehicle staggered departure, every station may have one pack per arriving vehicle.
P = 2T, T is vehicles. This case has one vehicle arriving for every station pack.
Swap Rate and Round Trip Chain
A round trip chain may be started in a route with vehicles returning from destinations.
The swap rate, is just the number of swaps Swap divided by time.
Swap Rate = Swap/t
Swap chain dynamics are not limited by charging time, for the slow charged swap case. Instead, they are mainly limited by the number of packs available. Since swaps take time, whereas charging may be simultaneous with number of chargers, in detail, swap time does stagger swaps and swap station charging. With waiting multiple vehicles served, depleted packs are gathered at swap intervals. Slow charged pack charge completion happens at staggered times equal to swap time. With limited packs, the first packs are accessed, then charge chaining can proceed with similar dynamics to the fast charge case. Fast charge chaining also exhibits staggered times if waits happen.
The number of swaps possible in the interval between station driving times, St, is just station interval time, Sd, divided by swap time, St.
Swaps = Sd/St, the next lower whole number.
Since swap times may be in minutes, and driving times at full range may be in hours, the number of vehicles stuffed into a chain can be high with unlimited packs, increasing the number of vehicles with the number of packs, one per vehicle and one per vehicle per swap station. The maximum vehicle capacity, Tmax, scales with packs and stations.
Tmax = (Pstation) x S, with all stations stuffed with vehicles.
or Tmax is equal to the number of Packs per Station (Pstation) x the number of Stations, S. In this case with simultaneous arrivals, Pstation is also the number of simultaneous arriving vehicles.
Station Utilization Efficiency
With simultaneous arrival of all vehicles at one station, and all other stations empty, utilization is low, with all stations designed for peak simultaneous swap,
P = S x (T + 1), for simultaneous arrival at only one station, with multiple empty stations en route. This is a bad utilization case, probably worse than real world.
Better planning would have vehicle departure staggered at intervals related to range and station distance. That could put one vehicle per station, and the number of packs required would be less. This would be a case of one pack per station with one vehicle arriving at each station.
For T vehicles, staggered single departure, T = S, and P = 2T
If there are simultaneous departures at staggered intervals continuously, arrivals can be expanded, such that there are always two packs per vehicle, one on the vehicle, and one at the swap station, and
P = 2T, at full utilization, multiple, staggered vehicle departures.
Result:
The relationship between number of packs and vehicles depends on swap station utilization. If utilization is 100%, P = 2T and every station has the same number of packs, and every station is filled at each swap.
In general, if it is arranged so that vehicles are arriving at all stations with the number of vehicles arriving equal to the number of packs, then
P = 2T
With staggered departures, stations are fully utilized.
Route Stuffing
Route stuffing is planning stations such that multiple vehicles are en route between stations. It is possible to design stations so that route stuffing is possible. For fast charging stations, the limit without wait is related to the charging time and driving time between stations.
The maximum number of trucks, Tchain, that the route can handle is:
Tchain = St/Ct = Sd/(v x Ct); Ct is charging time, v is velocity the speed limit, Sd station distance, and Tchain is a whole number dropping remainder. Since the limit of station distance is R,
Tchain < R/(v x Ct)
For swap stations, this is also the case. By charging in less time than vehicle arrivals, more than one group or single vehicle may be positioned between stations. Charging speed must be balanced with power demand. By stuffing the route between stations, the number of chargers or packs per vehicle can be reduced.
Peak Power
Peak power is a consideration for vehicle power. Stations are peak power limited. They may employ stationary buffer storage to reduce peak power demand. Fast charger power scales with the number of chargers and the speed of charging. Swap charging may be slow or fast. Swap station power depends on the number of simultaneous packs charging, and the charging rate. With multiple chargers, the peak power demand is just the sum of charger power.
With full utilization, one group of vehicles en route between stations, Swap P = 2T.
If packs are all slow charged, then charging time <= driving time.
Driving time = Range/v , where v is vehicle speed, the power is:
Peak Power = (Pack Capacity ( kWh )/ St )x Ps; where St is driving time between stations, Ps the number of packs per swap stations.
If the route is stuffed with more vehicles,
For fast charge, P = T without buffer storage. Peak power is given by number of stations, S, chargers per station, Cs, and charger power.
Peak Power = S x Cs x Charger Power = S x Cs x Pack Capacity/Charging Time
Charging time = Pack Capacity (kWh)/Charger Power(kW)
For swap, routes cannot be stuffed if slow charging is timed so that station driving time limits charge rate. If charge rate is increased, route stuffing comes at the expense of increased peak power. For fast charge, peak power is fixed. Stuffing reaches a limit with charging time.
In general, for fast charge versus slow charged swap, peak power is a function of simultaneous fast charge or per station, or number of packs per station, Ps.
Cs = Ps
The ratio of peak power between swap and fast charge is:
Pfc/Psw = St/Ct , where St is station driving time, Ct is fast charge time.
Pfc = Fast Charge Power
Psw = Swap Power
This simply says two things. The faster the charging, the more vehicles can be charged per charger. The faster the charging, the greater the peak power. Swap uses the driving time between stations to charge swap packs slowly.
Swap Station Continuous Operation
If swap stations have sufficient pack storage, they can reach a continuous output rate.
For example, if a swap station uses fast charge of 40 minutes, and there are 8 packs stored, and it has 5 minute swap capability, then it can operate continuously delivering packs at 5 minute intervals nonstop. At start, all packs are already charged. As the process continues, the first pack is swapped and starts charging. At each stage, another pack is swapped. By the time the eighth pack is delivered, the first swapped pack is fully charged and successive packs complete charging just before the next swap.
In general, continuous swap operation exists if the number of packs stored, P, is proportional the ratio of charge time, Ct, versus swap time, Swt.
P = Ct / Swt
Latent Traffic Staggering, Spreading
Traffic is staggered by any event that limits simultaneous or coincident movement. In particular, waits or bottlenecks cause traffic staggering or spreading. For example, if multiple vehicles arrive at a station and a single charger is in use, all vehicles wait for that charger, then charge one at a time and leave one at a time. Swap stations have a small staggering with swap time. Other examples of spreading are rest stops, traffic lights, onramps, bridges, lanes narrowing, and any traffic congestion. Roads themselves spread traffic, simply because vehicles cannot occupy the same space. Even at vehicle depots, or work parking lots, vehicles cannot exit at the same time, but are metered out by single lane exits.
Extended Route Networks
Other networks can be analyzed by extension from line networks using superposition. At node intersections, the number of chargers or swap packs for no waits increases with traffic. For star networks, the center point becomes the origin of a line. Mesh networks are an extension of line networks including intersections. There can be stubs, routes that are endpoints. There can be planning for depots and overnight slow charging according to schedules. The networks can be planned according to charging type required. The selection of chargers can also be made according to expected vehicle frequency.
Station Planning via Vehicle Route Frequency
While the analysis of required station, pack, and charger infrastructure shows requirements per vehicle, route station plan decisions can be made on the basis of vehicle frequency along routes. Vehicle travel frequency must be added to the analysis of charger, station, and packs per vehicle and utilization. The analysis shows that continuous staggered departures at intervals related to station distance optimizes utilization, putting vehicles at every station. From a frequency perspective, frequency distributions come into play. Planning decisions are made on the basis of vehicle frequency along routes, costs, and payback. If full utilization may not happen all day long, it may be acceptable if all stations, chargers, or station packs get used at some frequency or time interval during the day. An analysis of frequency of charger and station pack use can be the basis of decisions of cost versus wait times, in adding additional packs or chargers. It can also guide the decision whether to electrify a route with stations or not.
A simultaneous departure may have vehicles spread out as they split off the main roads. The number of stations and chargers will decrease as routes branch.
A network may be designed for a fleet of vehicles filling the network at full optimum capacity with one charger per truck or two packs per truck. Route stuffing may increase trucks per charger or per pack, at the price of faster charging and greater power. If simultaneous charge request or swap packs are insufficient, wait is the result. Some amount of underutilization may also be tolerated. Station expansion for rare events results in underutilization.
Have a tip for CleanTechnica? Want to advertise? Want to suggest a guest for our CleanTech Talk podcast? Contact us here.
Sign up for our daily newsletter for 15 new cleantech stories a day. Or sign up for our weekly one if daily is too frequent.
CleanTechnica uses affiliate links. See our policy here.
CleanTechnica’s Comment Policy