Compressed Gas For Electricity Storage Claims Are Mostly Hot Air – CleanTechnica

Sign up for daily news updates from CleanTechnica on email. Or follow us on Google News!

---

Three years ago, I published my projection of grid storage demand and solutions through 2060. At the time, various compressed gas electricity storage solutions such as compressed air, liquid air, and liquid carbon dioxide were in my also-ran technologies. My review of the literature over the preceding years had made it clear to me that they had intractable efficiency challenges and siting constraints, and as such wouldn’t scale.

But that was an outside view. Subsequently, I’ve been spending a lot more time on thermodynamics and operational requirements of solutions, and even a professional engagement assessing a compressed gas solution. Yes, they knew I was skeptical and STEM-oriented, and they wanted that.

Some Context For Compressing Gases For Energy Storage

Compressing gases and making useful energy out of them is one of those deeply intuitive solutions, so intuitive that it seduces people every decade into thinking that they’ve magically found something others haven’t. It’s also useful for seducing money out of gullible people’s pockets for much the same reason.

After all, our lungs compress gases and allow us to blow out a stream of air that can blow out a birthday candle. Anyone who has ever played with balloons has at least once blown one up and not tied it off but simply let it go to watch it buzz around in the air, defying gravity until it’s a small and shriveled rubber sack again. We pump air into bicycle and car tires, making them both firm and flexible, and witness the sometimes explosive results of tires failing.

We’re used to moving air being able to do work, from the foil or paper pinwheels we play with as children spinning when we blow on them to the wind turbines that are such a significant portion of new electrical generation. Many of us know — some quite vaguely, some in staggering detail — that nuclear and coal power plants are simply making gases that want to expand and harnessing their expansion to make electricity.

Of course, then there are pneumatically-powered actuators, where compressed gases make mechanical objects move. The first, in the west at least, were built in Paris in the 1870s, where a clock used pneumatics initially, and then a compressed air system was used to distribute power to industrial sites for their pneumatic actuators. For those in the trades, pneumatic nail guns and jackhammers are still daily tools.

And from a grid storage perspective, there are actually systems in place which have been working for decades, which does tend to lend a gloss of seriousness to the solution. The oldest electrical storage system I’m aware of was built in Germany in the 1970s, capable of storing 580 MWh and delivering it over two hours, leveraging a salt dome cavern. In the USA, a facility was built in Alabama in the early 1990s capable of delivering 2,860 MWh over 26 hours, built around a cavern that had been hollowed out of a salt formation. As a bit of foreshadowing, the two facilities are 42% and 54% efficient at returning electricity that’s put into them.

In recent years, a couple of variants have emerged. In looking at the constraints of compressed air storage and the basics of thermodynamics, some bright lights realized a lot more potential mechanical energy could be stored in a much smaller place if the gas were turned into a liquid and back to a gas in the process. As such, we now have many academics and startups working on liquid air and liquid carbon dioxide energy storage. Energy Dome is perhaps the best known of them, with its inflatable tennis court of gaseous carbon dioxide storage and claims of humbly being the only solution to long-duration grid storage and miraculously using the greenhouse gas to solve the problems it creates.

Two rules of thumb for red flags: If a firm claims both humility and asserts that it’s the only possible solution to a major problem, perhaps you should look at it skeptically. Second, if a firm is claiming to use carbon dioxide in a miraculous new way that will solve climate change, understand that there have been an enormous number of carbon capture, usage, and sequestration competitions, grants, and venture capital funds that have led to a rather absurd number of dead end firms having a lot of money based on their pitches, not their actual prospects.

Thermodynamics & Compressing Gases

Let’s start with the thermodynamics. I’ve dug through Grossman’s Thermodynamics: Four Laws That Move the Universe, three times and counting. As he notes during the early part of the material, the first time you work through the four laws, you don’t understand them. The second time, it’s all clear. The third time, it’s back to bewilderment.

The simplest statement of the laws is C.P. Snow’s:

1. You can’t win
2. You can’t break even
3. You can’t get out of the game

Imagine you are playing, as I have, Texas Hold’Em poker at a ring game in the Bicycle Club in Los Angeles. Every hand of cards that gets played sees the casino taking a few chips off the table to pay for the dealer, security, enhanced oxygen, lack of windows, overstimulating lights, and other less visible benefits for other people. That’s the rake.

In this game, no one can leave the table (law #3). As a result, the total number of chips keeps diminishing as the house takes its rake every hand. Everybody, no matter how much they win, eventually gives it all to the house. You can’t win (#1). You can’t break even (#2).

The first law, more frequently stated as energy can neither be created nor destroyed, is all about heat. The second law, for a spontaneous process, the entropy of the universe increases, introduces work. Every time work gets done, the house takes its rake, and that’s entropy.

Of course, even sleep-dulled eyes that have been playing far too much online poker — along with casino games, that hobby is in my past as well — will note that it’s four laws, yet only three are commonly listed. Yes, those wacky thermodynamicists have a zeroth law which rarely gets mentioned, if two thermodynamic systems are both in thermal equilibrium with a third system, then the two systems are in thermal equilibrium.

Imagine three poker chips floating in a row in space, a $20, a $100, and a $1,000. The $20 and the $100 are touching. The $100 and the $1,000 are touching. The $20 and the $1,000 are not touching. Because some chips are touching, eventually they are going to be the same temperature as the ones that they are touching, i.e. in thermal equilibrium. If the $20 is the same temperature as the $100 and the $1,000 is the same temperature as the $100, then the $20 and the $1,000 are the same temperature, hence in thermal equilibrium.

Heat wants to move to places with less heat because that increases entropy, and the universe loves entropy as much as it abhors a vacuum.

One of the things that comes out of all of this is that heat is not equal to work. Both are forms of energy, but while work can turn into heat with high efficiency, heat can’t turn into work with high efficiency. That’s the fundamental gotcha of fossil fuels and indeed anything we burn. What we are doing when we are burning something is turning it into heat, and if we need work, we lose a lot in translation.

A term that’s used in this space is exergy. Exergy is energy that can do work efficiently. Electricity has high exergy in that it can do both work and create heat with high efficiency. Heat has low exergy because it provides heat but loses a lot of the energy to waste heat when it’s used to do work.

That’s why gas and coal electrical generation plants are fundamentally limited in efficiency. They create heat to expand gases to drive pistons or spin turbines to create rotation to spin wrapped wires through a magnetic field to create electricity. That’s why internal combustion engines only turn 20% of the heat energy in gasoline or diesel into forward motion or work. They burn vaporized fuels in sealed chambers to cause expansion which makes the piston move out and through mechanical linkages turn gears which connect to wheels.

The second law, you can’t break even, means that every time you do work you create at least a little bit of heat, and you can’t get that back efficiently. That’s entropy, the thermodynamic casino’s rake.

What does this have to do with compressing gases to store electricity? Well, compression is work. Compressing a gas creates higher pressure gases which want to expand. That creates mechanical potential energy, something that can be used to create work to spin turbines to generate electricity as the expanding gases rush through the device. But it also creates heat — sometimes a very great deal of heat.

The ratio of the created mechanical potential energy to the heat is a fundamental drawback of compressed gas electricity storage solutions. If you want a lot of mechanical potential energy, you end up creating an awful lot of heat. If you want to avoid losing all of that energy to heat, you end up without much mechanical potential energy.

There have been a lot of organizations trying to square this circle for decades, but the basics of thermodynamics and gases have been well understood for a couple of hundred years and aren’t changing. If the universe is a casino, the laws of thermodynamics are immutable regulations for how the game is played.

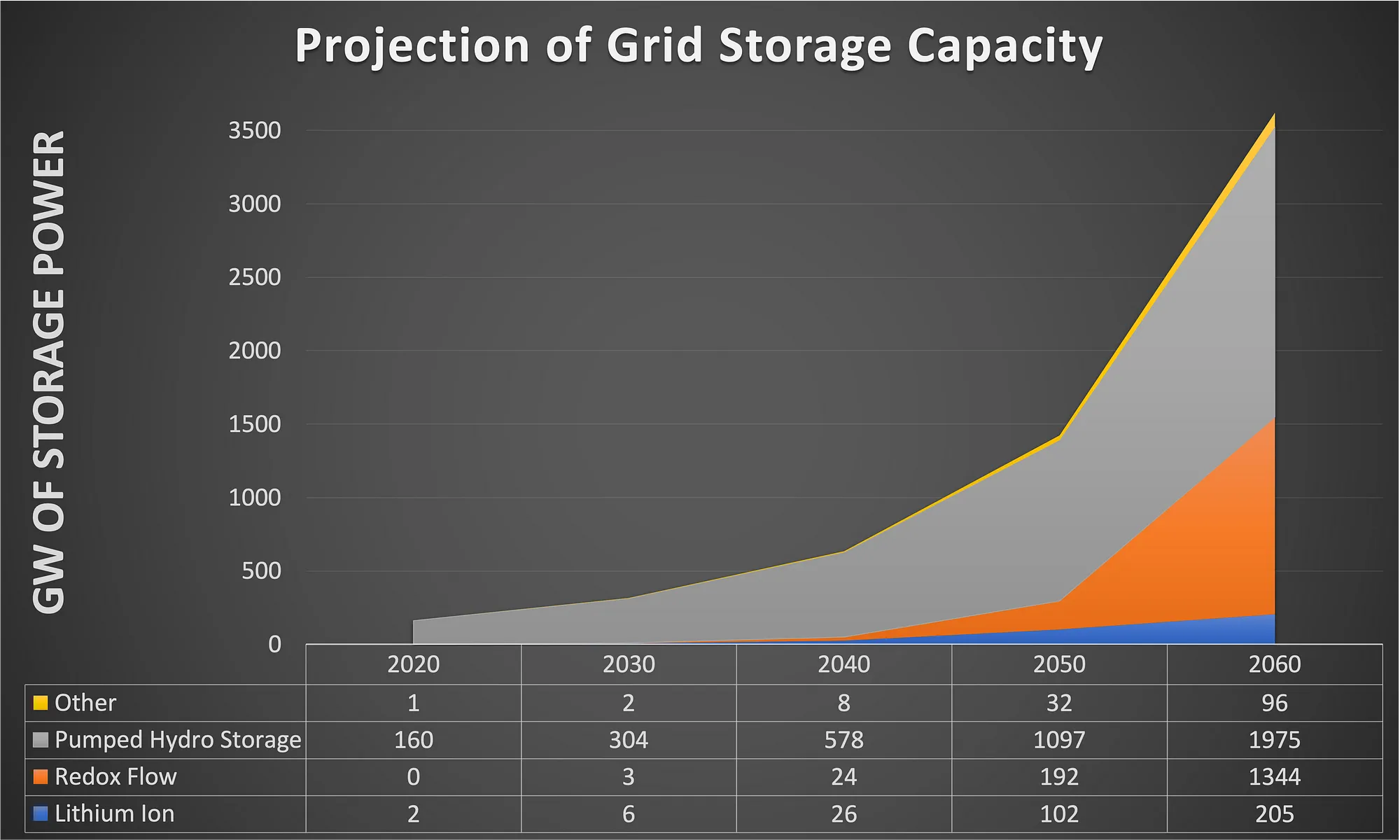
How have people tried to cheat the system? Well, that’s where phase diagrams, another staple of thermodynamics, come in. What’s a phase diagram? The most common form is simply a chart of what phase a substance is in at different temperature and pressure combinations.

Let’s start with something we all are familiar with — water.

Everyone knows that water freezes at 0° Celsius or 32° Fahrenheit. That point can be clearly seen on the diagram above, where at 0° Celsius and one atmosphere, there’s a conversion from one phase of the substance we know as water to another, liquid to solid or the reverse. But you’ll note that water can stay a liquid below that temperature under higher pressures.

And we all know that water boils at 100° Celsius or 212° Fahrenheit (although I’d completely forgotten the Imperial and had to look it up just now). But water can boil at much lower temperatures as pressure decreases, something people who live in Santa Fe or who have ever tried to make a hot drink at the top of a mountain know very well.

The phase of water, whether it’s solid (ice), liquid, or gas, depends on the combination of temperature and pressure. We just happen to live in the range of pressures and temperatures where we commonly see it turn from one to another. Every substance is like this.

Note that pressure tends to be denoted in a logarithmic scale. That’s because pressure units tend to get very big very fast compared to temperature units, so most phase diagrams would be a meter tall and ten centimeters wide. The logarithmic scale just multiplies every increment by ten, so it goes 1 to 10 to 100 to 1,000 on the vertical axis of the chart.

There’s something else worth pointing out on the diagram, at the upper right-hand corner. Water can also be in a supercritical phase where it shares the properties of both gases and liquids. You need pretty extreme pressures and temperatures to get there, 218 atmospheres and 374° Celsius, but some supercritical fluids are very useful.

Here’s the thing about phase changes: every change in phase requires an awful lot of heat, a lot more heat than required to make something tens of degrees warmer or colder in the same state. When water freezes, the temperature isn’t a straight line, but it plateaus at 0° Celsius for quite a while as more and more heat is sucked out of the liquid, then ice starts forming. Similarly, warming up ice brings it up to 0° Celsius pretty quickly, but then it just sits there for a long time absorbing heat until water starts forming. That’s why ice cubes keep our drinks cold for a long time.

There’s a lot of stuff happening at the molecular level in terms of hydrogen bonds forming between water molecules that occurs around phase changes and that’s where all the energy is coming from or going to. Solids are highly ordered structures with only vibrational energy within molecules — think of an absurdly fast oscillating spring between two balls where the balls are atoms and the string is the chemical bond — and no rotational or movement energy. Liquids have additional rotational and movement energy because the bonds between molecules are less structured and tight. Gases have lots of rotational and movement energy as there are no chemical bonds between molecules keeping them together. All of the heat that creates a phase change goes into breaking the chemical bonds.

The phase change of water from a liquid to a gas is what we use in coal and nuclear plants. Pumping heat into water until it turns into steam has an advantage in that gases are much more diffuse. Pumping heat into water until it turns into steam creates mechanical potential energy due to the steam wanting to expand a lot. We capture that energy by pushing the steam through a turbine to spin it to create useful electricity, using the expanding steam to create work which we can harvest.

If you look at the phase diagram for water above, you can see that there’s an intersection point of straight lines drawn on it at 1 atmosphere and 60° Celsius. If you track to the right, you’ll see that at 0° Celsius there’s a phase boundary and ice is on the other side of it. If you track to the left, you’ll see another phase boundary at 100° Celsius and gaseous water, steam, is on the other side of it. Putting heat into water warms it to 100°, and then a lot more energy is used to shove it over the phase boundary into steam.

How much? Let’s imagine a basic case. A coal or nuclear plant takes room temperature water and turns it into steam. It takes eight times as much energy to move from 100° Celsius water to 100° Celsius steam as it does to heat water from 20° to 100°. We get a gas that is much higher pressure than the water and can exploit that to do work, but we can’t get the heat back that was used to create the gas. As a bit more foreshadowing, any solution which depends on a phase change and is supposed to be doing work to create electricity is stumbling badly over this tripping point of thermodynamics.

Compressed Air Storage

There are four compressed gas electricity storage solutions that tend to get all the press — compressed air, liquid air, liquid carbon dioxide, and supercritical carbon dioxide. They all have different acronyms and there are some firms which devote inordinate time and get inordinate investor funds for them, like Energy Dome for example. Certainly the US Department of Energy has spent far too much time and money on one of the variants over the past few decades with nothing to show for it.

As noted, the only one in commercial use in a tiny number of instances is compressed air storage. It has three to four very big advantages over the other solutions, yet isn’t scaling.

What are the big advantages? To start with, the container for the uncompressed gas is our atmosphere. The only thing that needs to be built is a the airtight tank for the compressed gases. Second, the gas is free because it’s just the air that we breathe. Third, it avoids changing phases, pressurizing the air to around 75 atmospheres, the equivalent of about 750 meters beneath the sea. That avoids that big energy loss due to the heat required for changing phases.

It also has the advantage of not changing the fundamental characteristics of the gas into something that messes badly with the process and technology. When we change the phases of substances, odd things happen. For example, liquid carbon dioxide with traces of water is much more corrosive than gaseous carbon dioxide and water vapor.

The exergy of compressed air is what seduces thermodynamicists, if not engineers. Let’s explore this a bit. Remember that it’s the ratio between the potential mechanical energy that’s created versus the heat that’s lost that’s important. We want to create a lot of potential energy while creating as little heat as possible.

Thankfully, we stand on the shoulders of giants, so there is simple math for all of this. The basic formulas are:

• Work = average pressure * ( initial volume – final volume )
  simplification of the ideal gas law
• Heat = initial enthalpy – final enthalpy
  enthalpy = total heat content of a system

If we know the attributes of a substance at a particular temperature and pressure and we want to move it to a different temperature and pressure, these formulas tell us how much energy is required. When we compress a gas, we have to expend a lot of work, but we also create a lot of heat. When we expand a gas, we get a lot of potential for work but we also require a lot of heat.

For compressed air, we start at room temperature and end at room temperature for convenience, just changing the pressure. We want to keep the air a gas so we don’t eat the phase change energy loss.

Air, the atmosphere that we breathe, is 78% nitrogen, 21% oxygen, and a bunch of trace elements, some of which like carbon dioxide, methane, and hydrofluorocarbons are much more consequential than others due to their ability to trap infrared. Nitrogen being the biggest component in the solution we call air, I’m going to cheat a bit and talk about pressurizing nitrogen.

At room temperature and pressure, nitrogen has a density of about 1.2 kilograms per cubic meter, so a ton occupies about 870 cubic meters. At 75 atmospheres, it has a density of 86.7 kilograms per cubic meter, so the same nitrogen only takes up 11.5 cubic meters. When we let the nitrogen expand, we can take the average pressure of 38 atmospheres and multiply it by the difference to find out how much work was done, about 905 kWh. That’s also the potential mechanical energy we get back assuming a 100% efficient system.

What about the heat? As the italics above note, enthalpy is the heat content of a system at a particular state, which is not the same as its temperature. For convenience I’m going to stick to kWh, but remember that a kWh of heat is not the same as a kWh of electricity. The difference in enthalpy is only 4.4 kWh. That means that the ratio of mechanical energy to waste heat is 99.5% at this degree of pressure change. That’s a good ratio.

That’s the kind of finding that excites a thermodynamicist who hasn’t spent a lot of time with system efficiencies and infrastructure costing. It’s a seductive number and explains why a couple, but only a couple, of quite big electricity storage solutions have been built. We’ll get into the next bits shortly, but let’s digress out of gases.

That gives compressed air some advantages over other compressed or liquid gases, but how does it compare to another long-standing energy storage solution, pumped hydro? The advantage of water is that it just sits there at temperatures and pressures on the face of the earth. We don’t have to find or create an airtight cavern, we just have to dig a hole and pour water into it. That’s convenient. It’s a lot cheaper and easier to build holes than caverns, although water excavation of salt caverns is also a very mature and not that expensive approach, assuming you have a lot of salt deposits underground at reasonable depths as many places like the southeast of the UK do.

Both compressed air storage and pumped hydro have some geographical limitations, but as I keep pointing out, the places with 400 meters of elevation change within a couple of kilometers of one another — the geographical constraint on closed loop, off-river, pumped hydro — is hardly unusual. The Australian National University’s greenfield atlas GIS study found 100 times the resource capacity as the total expected end-game requirement, 200 times in the USA.

Does water have any other advantages over gases when it comes to returning mechanical energy? Yes, in fact. It’s more efficient to pump water and spin turbines with water than to compress gases and spin turbines with gases. Once again, this is due to the characteristics of materials in phases, with water having chemical bonds that means it wants to stay together while gases don’t have those chemical bonds. While there’s a loss of about 10% each way in pumped hydro, there are losses in the range of 20% or more each way with compressed air.

The best case theoretical numbers I’ve seen for compressed air storage are 67% round trip efficiency, and the existing solutions are running at 42% and 54% efficiency in real world solutions. The spreadsheet I put together underneath all of this suggests a maximum theoretical efficiency of just under 62%. To be blunt, there’s nothing magical about compression and turbines for pressurized gases that has advanced a lot since the 1990s. This is very mature technology, especially at the pressures in question.

What About Liquid Air?

So compressed air storage has low real world efficiencies despite high apparent thermodynamic efficiency. It’s competing with another already massively scaled solution that’s being built in vast numbers of GW and GWh of capacity globally today — pumped hydro. It’s not winning. Naturally, people invested in compressing gases for electricity storage aren’t going to take this sitting down.

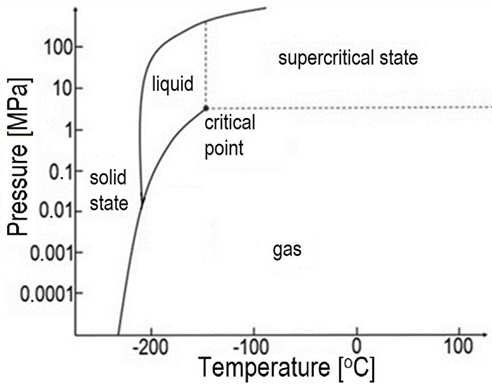
Sidebar: There are people with lovely phase diagram generator software that will normalize all units, but I don’t have access to them. While the Kelvin scale is the temperature scale for thermodynamics, Americans frequently insist on Fahrenheit and others who should probably know better use Celsius. Similarly, pressure is denoted in a stew of different units, in this case megapascals (MPa). Every megapascal is about 10 atmospheres.

They know that just on the other side of the phase change line there’s a much denser liquid. That increase in density means that as the liquid expands back into a gas, there’s an awful lot more potential energy to be harvested. Enter the world of liquid air energy storage. Once again I’m going to simplify this down to nitrogen, the dominant gas in the mixture, but as I noted earlier, that works for hypothetical models like this, but falls apart rapidly in the real world because as mixtures and solutions change phases, their characteristics change in often alarming ways. That’s part of the reason why some liquid air solutions are actually liquid nitrogen solutions, with another set of components that strip off everything that isn’t nitrogen from the air, increasing the cost of the basic resource.

As you look at the diagram, however, you might note something odd. There is no liquid nitrogen above -147 ° Celsius, no matter how high the pressure gets. In fact, at one atmosphere, about what you are feeling on your skin as you read this, liquid nitrogen only occurs at -195.8° Celsius.

That means that in order to take advantage of that extreme volume difference between the liquid and gas phases, you have to chill nitrogen from 20° Celsius to -200° Celsius or so, and keep taking heat out at that -195.8° Celsius phase change point for a long time.

What does this give you? A liquid that’s ten times as dense as nitrogen compressed to 75 atmospheres. That’s ten times as much mechanical potential energy in the same volume. That’s a seductive number again, which is why people keep throwing lots of money at this.

But remember, they are taking heat out of the nitrogen in order to create the liquid — a lot of heat. Taking a ton of nitrogen and liquifying it creates a potential mechanical energy of about 24 kWh, but requires taking out five times as much energy, 120 kWh, in the form of heat. The potential efficiency is only about 17%, ignoring anything else.

But like hydrogen for energy types, liquid air types are nothing if not persistent beyond all rational understanding. Heat may not be work, but it is heat and it can be stored, at least for a while. As I noted in an analysis of an ill-fated waste-to-energy waste heat to barge to district heating scheme proposed for London a while ago, one of obvious solutions for storing heat is in phase-change materials. So in addition to changing the phase of air from liquid to gas with rather ridiculous energy, another phase-change material is bolted onto the solution to return at least some of the heat.

Are there any other challenges for liquid air solutions compared to compressed air? Yes, in fact. The nice thing about putting compressed air in an underground cavern is that it doesn’t really care that the cavern is probably warmer than room temperature, as temperatures increase as you head deeper. 30° or 40° doesn’t really make a difference to compressed air. But liquid nitrogen would suck all of the heat out of the walls of the caverns, which in turn would suck all the heat out of the surrounding area and the surrounding area is vastly bigger and with higher heat energy than the cavern and liquid nitrogen. No salt caverns for liquid air solutions, so no high volume cheap places to put liquid nitrogen.

Liquid air solutions need highly insulated constructed tanks, which once again limits their ability to scale compared to compressed air and pumped hydro.

The efficiency losses of all of that heat transfer are then multiplied by the efficiency losses of turbines that run on gases. While the industry claims up to 70% efficiency is theoretically possible, in practice they are running under 50% again, below the threshold where they are competitive. The combination of low efficiencies and increased capital costs for storage make it hard to imagine it having an economic value proposition.

And So To Liquid Carbon Dioxide

Energy Dome and other players in this field forego the advantages of using the air we breath as the basic unit of storage. They claim that this is an advantage, but that’s hype, not economic reality. By now you know the drill, so I’ll get into it.

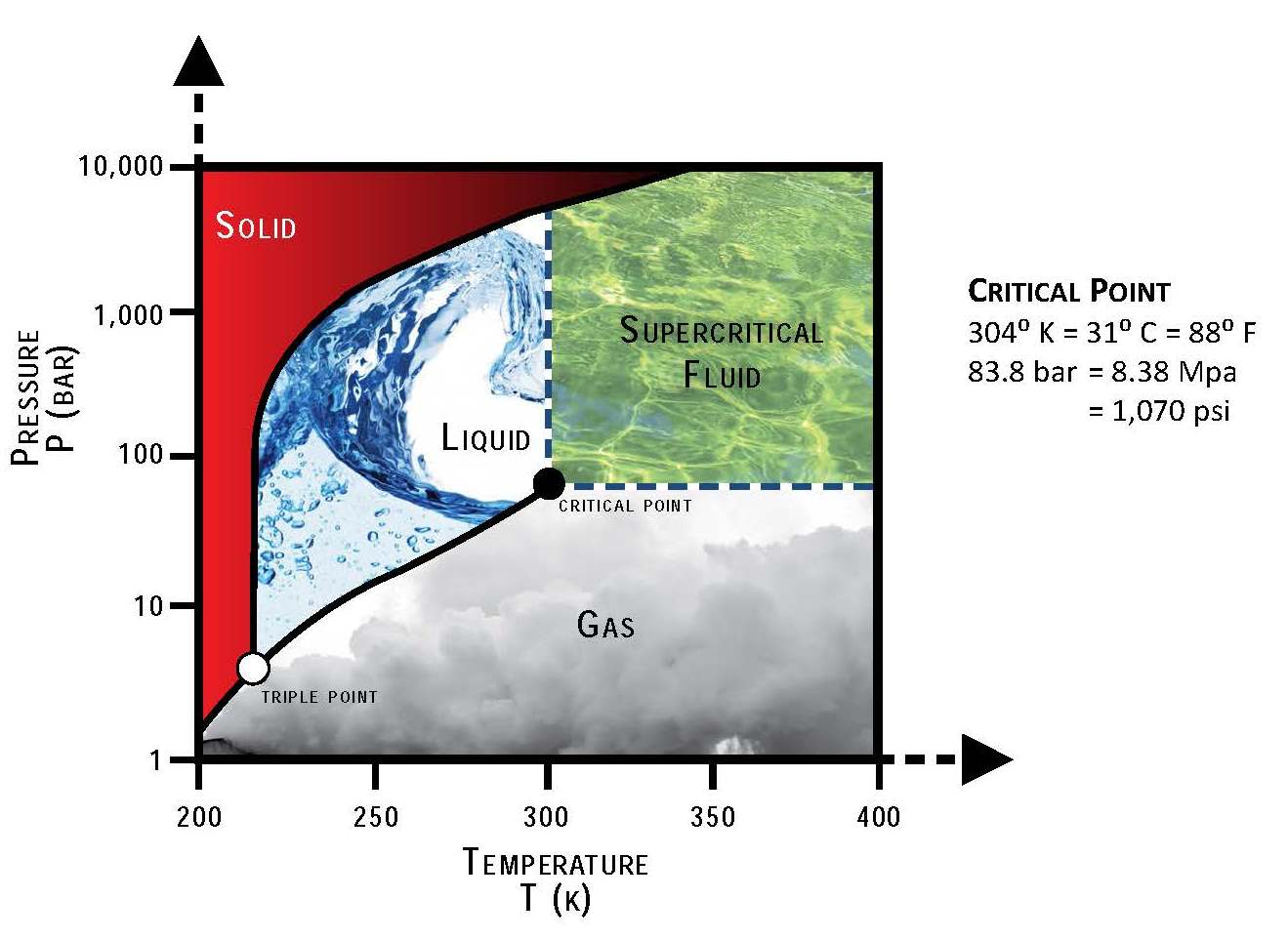
Once again, units. A bar is about equal to an atmosphere, so it’s something we can grasp. And Kelvin is the same scale of individual as Celsius but starting at absolute zero, -273.15° Celsius. Subtract about 300° from any Kelvin number and you’ll get a hot summer day in most parts of the world in Celsius.

That 20° Celsius gas is a 293° Kelvin gas. At that temperature, about 57 bar or atmospheres of pressure will shift it to a liquid. Density of the liquid is about 470 times higher, so there’s a lot of mechanical energy to play with, about 380 kWh. But the phase change eats a lot of heat energy, about 84 kWh. The maximum thermodynamic efficiency is only about 82%.

Add in the other losses for gas compression efficiency, providing the heat to turn the liquid back into a gas, then the inefficiencies of turbines for gases and the roundtrip efficiency is well under 50% again. Bolt on thermal storage again and you might get the efficiency up above 50% in the real world. Energy Dome claims 75%, which frankly doesn’t seem realistic and is unsupported by third party certified testing or any actual deployed units. They might, just might, get up to 60% in the real world.

Are there any other challenges with solutions like this? Well, yes, it requires fairly pure carbon dioxide. Remember that liquid carbon dioxide with only small amounts of water is quite corrosive. That means that they have to maintain a fairly pure supply of gaseous carbon dioxide on one side of the equation, hence the thing that looks like an inflatable tennis court in their renderings.

Unfortunately, that has limits. Gaseous carbon dioxide may be denser than the air we breathe, but that doesn’t mean it’s dense. Inflated air structures like sports domes and the very large ones keeping coal dry in a couple of places are only slightly overpressurized, not vastly different than the outside air. A ton of slightly pressurized carbon dioxide would take up about 500 cubic meters.

The biggest inflated structure in the world, a coal storage facility, is about 53,000 square meters. Assuming it’s longer than tall and about 20 meters high, the volume would be around 740,000 cubic meters. That would contain just under 1,500 tons of carbon dioxide and might be able to hold 250 MWh of electricity. That’s for a structure about three-quarters of a kilometer long and a hundred meters wide, which is to say, huge.

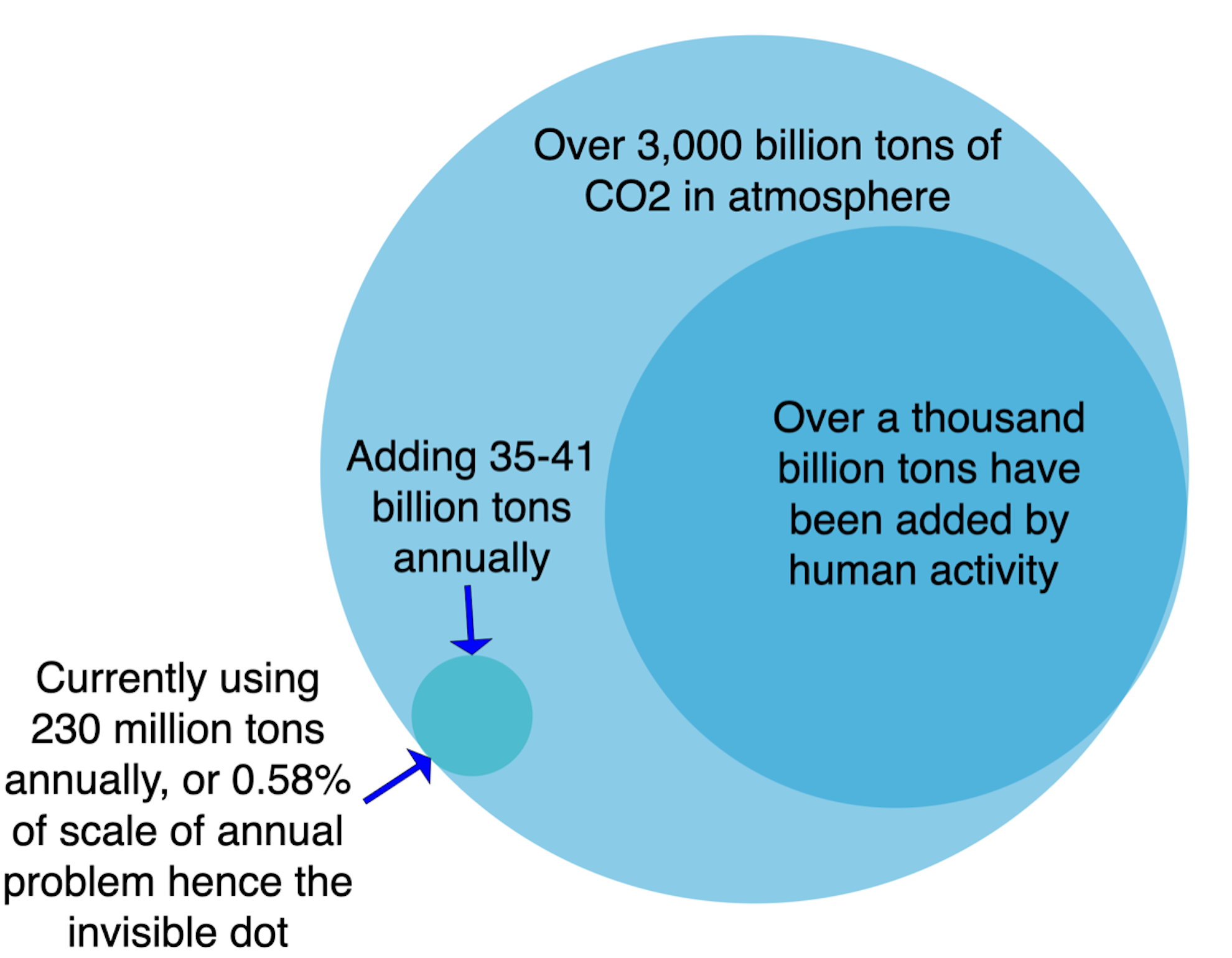
I like to use this chart when talking about carbon dioxide usage schemes. The scale of the problem is thousands of billions of tons. The annually additions are tens of billions of tons. The annual current market is about a couple of hundred million tons and it’s a rounding error on an emaciated gnat’s thorax compared to the scale of the problem. Imagine my sentiments about 1,500 tons, many more orders of magnitude less, as a carbon dioxide usage solution.

Anything else? Why yes. Inflated air structures have lifespans of 15 to 20 years, not the 30 years that Energy Dome asserts. Getting to 20 years requires constant pressure to avoid stresses on the composite fabrics. Even then, solar radiation is hard on these kinds of structures, so they don’t last as long as permanent structures. Daily pressurizing and depressurizing, the requirement for a gas to liquid to gas storage solution, is the opposite of constant pressure. My assumption is that the actual lifespan of one of these domes would be under 10 years, perhaps even only five years.

Is there any way around this? Sure, you could store the gaseous carbon dioxide in a salt cavern instead of a tennis court. That would enable higher pressure gaseous carbon dioxide storage too, so even though a big manufactured salt cavern might only be a bit bigger than the inflated coal dome in the example, it could store a lot more carbon dioxide.

Imagine putting 40 atmospheres of carbon dioxide gas being converted to liquid and back. That must work out better in terms of energy, right? Well, no. The ratio of heat to work plummets. In this case of 40 atmosphere gas to 57 atmosphere liquid and back, the theoretical maximum thermodynamic efficiency is only 11.1% and the actual end game efficiency is probably only 5%. The phase change soaks up all of the advantages and more.

Be Supercritical Of Supercritical Carbon Dioxide

Very smart people often persist in exploring every possible pathway, long after normal people have given up and built pumped hydro and battery storage. Such is the case with compressed gas energy storage types. Is there anywhere else on the phase diagram to explore?

In the upper right hand corner of the diagram is the supercritical phase. It’s an interesting state that has some of the characteristics of a liquid and some of a gas. There are some optimal points in there where moving between two pressures and temperatures doesn’t require a lot of energy but does result in large material density swings. Slap a turbine between the two ends of the cycle and it’s more like generating electricity from a liquid. That’s a seductive notion, energy for nothing and your kWh for free.

This is a dream that’s been with energy types for decades. The first prototype of a supercritical CO2 Brayton cycle generator was built in 1948. That’s 76 years ago. The US Department of Energy has thrown probably hundreds of millions of dollars at it since. It resurfaces regularly as the next hope because the generators could be so much smaller for so much more power generation, among many other deeply optimistic projections.

The reality of the gas-fluid state is that it sucks for turbines. The gas bit means that there are no bonds between the molecules so they all have to be shoveled through a higher velocity turbine like one that works with steam. The higher velocity means much sharper veins moving much faster. The liquid aspects means that those fragile blades keep smashing into denser molecules. That means that they keep pitting and abrading.

76 years of materials science hasn’t solved this or other problems. It remains in the labs, grant applications, and research programs, and resurfaces in venture capitalists’ portfolios every decade or so. It seems to be having another moment in the sun now, but the clouds of reality will roll in again.

Compressed Gas Storage Is Mostly Hot Air

So that’s a brief trot through the compressed gas storage space, looking at the solutions, why they fall over, and the various efforts of bright people to come up with some variant that doesn’t fall over. Compressed air just isn’t that efficient, needs a big salt cavern, and can’t compete with obvious alternatives. Liquid air fails due to thermal management and the efficiencies of turbines for gases. Liquid carbon dioxide fails because of phase change thermodynamics, storing all that gaseous carbon dioxide, and the efficiencies of turbines for gases. Supercritical carbon dioxide fails because it destroys turbines.

If there were no other alternatives, I’d be happy enough with a bunch of salt caverns and compressed air storage. It’s the mediocre best of a meh lot, low in efficiency but with fewer other compromises. Its ability to scale is limited, but there are a lot of salt deposits in various places.

But there are other alternatives, especially pumped hydro, which has many fewer compromises and a much greater ability to scale. Building a pond that can hold billions of liters of water is pretty easy, and every billion liters at 500 meters is a GWh of energy. That’s why China has 19 GW in operation, and 365 GW in construction or about to start. When seeking answers about what makes economic sense for low-carbon solutions, asking what China is actually scaling is always a good idea, and what it is scaling is pumped hydro.